自動分割メッシュのヒント

内容:

1.1 規格化座標と二次元グリッド番号
 1.2 メッシュブロック
 1.3 規格化座標から　実座標への射影
 1.4 サンプルコード1(C++)

1.1 規格化座標と二次元グリッド番号

簡単な二次元のメッシュ分割について議論します。
まず、一般の四辺形で表される二次元ブロック内を分割する場合を考えます。
多角形ブロックへの拡張は後に行います。

ブロック内を三角形メッシュで分割する方法は多く発表されていますので、ここでは四辺形要素で分割する方法を考えます。
但し、条件として四辺形ブロックの各辺に関する分割数は与えられているものとして内部を分割するものとします。

問題を簡単にするため、四辺形ブロックを位相幾何学的に分割します。　ここでは、分割の対象となる四辺形ブロックが(0,0)-(1.0)-(1,1)-(0,1)の頂点座標を持つと規定します。　以下、これを規格化された四辺形ブロックと呼びます。

規格化された四辺形ブロックには、あらかじめ各辺がn1,n2,n3,n4 に分割されていると仮定します。

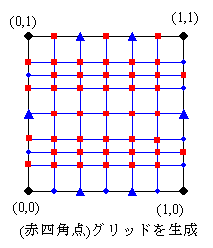
それぞれ、対辺の分割数の多い方の辺を元にしてグリッッド(赤四角点)を生成します。
このとき、規格化座標で一致する対辺の分割点は必ず一致させます。(青三角点)

分割プログラムを作るときは、このグリッド番号を二次元的なインデックスを持つ配列にします。

つまり、C++ で書きますと

class Grid {
　public:
　double x,y;
　void set(cost double _x,const double _y) { x=_x; y=_y; }
}

Grid　theGrids[20][20];

......
theGrids[0,0].set( 0.0,0.0 );
.......

こうすることにより、各辺にあるグリッド番号を簡単に見つけることができます。
たとえば、グリッドtheGrids[i][j]の両端点は
theGrids[0][j],theGrids[imax][j]　と　theGrids[i][0],theGrids[i][jmax]
になります。　　ここで、　imax = Max(n2,n4),　jmax = Max(n1,n3) です。

1.2 メッシュブロック

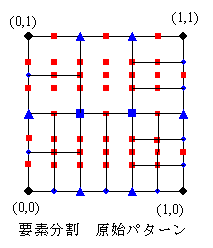
次の段階では、このブロックを青三角を頂点とした6個の小ブロックに分割します。
このとき、青四角も頂点として追加します。
要素分割を、外側の辺分割としてそのまま、採用しますと、左図のようになります。

不整合をなくすためには、ブロック間の中間節点を処理する必要があるのがわかります。

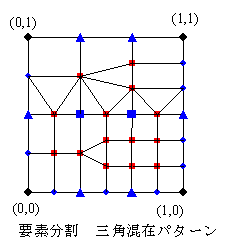
三角分割パターンを許すならば、分割は比較的単純で、たとえば左図のようなパターンになります。
左図の分割法は、小ブロック内で対辺の分割の違いを、分割数の少ないブロック側で三角形要素を採用し、整合させる方法です。

1.3 規格化座標から　実座標への射影

規格化座標から実座標へは、

四辺形ブロックが(0,0)-(1.0)-(1,1)-(0,1)の頂点座標の実座標　と
四辺の分割比率(実は規格化座標ですでに 0,1に規格化して先に決めておく)

が定まれば、決めることができます。

計算方法はいくつかありますが、以下のような制約条件や評価関数を設けるが妥当でしょう。

各辺の分割が、等差、等比あるいは任意与えられているので、四辺上ではその分割が保たれていること。　つまり、外辺上の分割は、入力条件であるので、変えてはいけないということ。　計算は内部の点のみ対象とすること。
限りなく、外辺に近い内側の分割点はその辺の分割点に近づくこと。　つまり、内→辺　極限値が辺上の分割点になること。
分割数・メッシュ間隔の変化が均一に近いこと。

1.に関しては守らねばならない制約条件です。　2. , 3. に関しては分割を評価する評価関数を作成する上での指針となります。

もっとも、簡単な方法は、規格化座標で、各辺の分割を等差、等比あるいは任意で与え、対辺を互いに直線で結び、その交点を内側の点とすることです。
その規格化座標での内側交点の座標を、直接射影して実交点を求めます。
射影に使う座標変換としては、

どちらか一方の成分で比例配分する方法。
4頂点の基にした面積座標を使う方法
同じ面積座標を使うにしても、交点の計算に使用した各辺上の点を使う方法。
また、面積座標ではなく、これらの点の重みを高さとして、三次元空間上の2次曲面として計算する方法
ポテンシャルやスプライン補完を使う方法があります。

1.4 サンプルコード1(C++)

1の方法は、一方向の情報しか使用しないのですが、次のように非常に簡単に計算できます。　その結果もまずまずです。

// V2.h ヘッダーファイルに定義
// Copyright 2001 (c) Shift Lock Corporation
// 二次元ベクトルクラス
class V2
{
  public:  double x,y;
  // コンストラクタとデストラクタ
  V2():x(0),y(0) {}
  V2( const double _x, const double _y=0 ):x(_x),y(_y) {}
  virtual ~V2() {}
  // セット
  void setXY( const double _x=0,const double _y=0 ) { x=_x; y=_y; }
  // コピーコンストラクタ
  V2( const V2& a )
    { copy(a); }
  // コピー
  void copy( const V2& a )
    { if( this!=&a ) { x=a.x; y=a.y; } }
  // 代入演算子
  const V2 operator = ( const V2& a )
    { copy(a);  return *this; }
  // 加算
  friend V2 operator + ( const V2& a, const V2& b )
    {  return V2( a.x + b.x, a.y + b.y ); }
  // 減算
  friend V2 operator - ( const V2& a, const V2& b )
    {  return V2( a.x - b.x, a.y - b.y ); }
  // スカラー倍
  V2 operator * ( double s ) const
    { return V2( x*s, y*s ); }
};

// .cpp ファイルに定義
#include "V2.h"

int main()
{
  V2 vN[5][8];// 規格化座標
　// ここの間で5X8 の規格化座標を作る

  V2 vR[5][8];// 実座標
　// ここの間で実座標は基準となる方向の相対する2辺の座標のみ与えておく
  // x方向を基準とするときは、辺2と辺4の分割実座標を与える。
  // y方向を基準とするときは、辺1と辺3の分割実座標を与える。

  for( int j=1;j<7;j++ )
  {
    V2 vL2 = vR[4][j];  // 辺2の分割実座標
    V2 vL4 = vR[0][j];  // 辺4の分割実座標
    for( int i=1;i<4;i++ )
    {
      V2 vP = vL2 - vL4;
      vP = vP*vN[i][j].x; // 規格化座標のx成分のみ使用
      vP = vP + vL4;
      vR[i][j] = vP;
    }
  }
  for( j=0;j<8;j++ )
    for( int i=0;i<5;i++ )
      printf("%lg,%lg \n",vR[i][j].x,vR[i][j].y );
  return 0;
}