電磁場解析ソフトウェアとは

　弊社のコンサルタント業務として得意とする電磁場解析についていろいろな話題を提供します。

電磁場解析へのアプローチ

はじめに

　これから、電磁場解析へのアプローチにはじまり、いろいろな話題を提供しようと思っているのですが、ここのページに来られた方は何らかの理由で、電磁場解析に関心を示すか、またはこれから電磁場解析しようとする方だと思います。　既に電磁場解析をしている方が、ちょっと覗いてみるのもいいかもしれません。

何故、電磁場解析が必要か?

　一言に電磁場解析といっても、現状の解析法・ソフトウェアははすべて電磁気現象を統一的に取り扱える訳ではなく、物理現象に応じて電場解析、磁場解析、電磁波解析に分けるのが一般的です。 (実際には、もっと細かく分かれます。)　将来的には、すべて統一的に扱えるソフトウェアが作られるかもしれませんが、まだまだ、コンピュータパワーが必要な分野で、20年後でもできるかどうか怪しいところです。　しかし、一般的にすべての電磁気的現象が取り扱えなくても、とりわけ関心のある現象のみ詳しく・精度よく解析することでも、結構、役に立ちます。

　

　いま抱えている問題が、果たして電磁場現象すべてが統一的に扱えないと計算できない問題なのか、電場解析・磁場解析・電磁波解析のどれかに分けて計算できるのか、あるいはこれから述べるように、もっと限定して計算できるのかによって、解決できるかどうか決まります。　大雑把に言えば、時空的に次元の多さ・モデル形状の複雑さ・物性的な複雑さなどがお互いにトレードオフの対象となります。 ここで、物性的な複雑さとしては、誘電体なのか、導体なのか、磁性体なのか、半導体なのかetc…があり、また別の分類としては、非線形性・異方性等があります。

　例えば、身近な磁気的現象を真面目にモデル化すると、すぐに3次元磁場解析で異方性のあるヒステリシスを考慮し、磁性体・導体の動きと渦電流も加えた問題となり、非常に難しい解析となります。　さらに、同時に誘電体が絡む変位電流を考慮するなどとなると動磁場と動電場を連成計算する必要があり、私の知る限りにおいてはこれらすべてを同時にまともに取り扱える汎用ソフトウェアは現状存在しません。　 (ここで、私が「3次元・汎用」と言っているのは、任意形状で計算できるものを指しており、モータ専用とか、トランス専用とか言うソフトウェア指しているものではありません。)

　ですから、電磁場解析に何を期待するのか、最初に明確にし、解決すべき問題への要求定義をはっきりさせなければなりません。　その後、求めるものと現状の解析法・ソフトウェアの限界との摺り合わせをすることになります。　もちろん、複数の解析法・ソフトウェアを利用すれば守備範囲は広くなります。　組み合わせによっては、かなり複雑な問題も解くことができるでしょう。　しかし、それには多くの経験と知識、多大なる労力と資力が必要です。　反面、問題となるべき現象と的確に捉え、モデルを限定するなどすれば、短時間に精度よく解が求まります。　どちらのアプローチをとるにせよ、職人肌的な要素がかなり色濃く残ってしまいます。　ここに、我々ソルバー開発メーカーの存在理由があるといっても過言でありません。 たとえ、AIが進化してきても、検証済みの膨大なデータがなければ学習させることができません。　　

　皆さんは、今抱えている問題が、本当に解けるのか?(満足できる解が出るのか)　まず知る必要があります。　場合によっては、電磁場解析より実験・実測の方が良い選択であることがあります。

　ずいぶん、否定的なことを書きましたが、あまりにも予備知識がなく、電磁場解析をやろう、またはやっている人が多いので、ここに書きました。　このコーナーは、そういう人たちのために、一助になればということでこれから構築した次第です。

精度が要求される電磁場解析

　電場・磁場の値は他の解析と比べて直接計測し易い一面(元々電気信号だから･･･)があるので、その解析精度は往々にして、厳しく要求されます。　また、電磁場解析の結果、直接得られる電場や磁場よりも、それを元に応力やトルクなど二次結果を求めることが多いので、一次計算結果である電場や磁場はかなり精度良く求めなくてはなりません。　

　例えば、磁場による応力は、磁場の二乗に比例し、トルクはその差で求まりますので、有効数字が極端に少なくなることがあります。　磁束密度の誤差が5パーセントでも、力やトルクの誤差は100パーセントなんてこともあります。　　最近では、磁場測定値から、逆に物性値(渦電流等から電導率)を求めるという　いわゆる逆解析(感度解析)などもあります。 このような場合も、わずかな磁場の変化から、物性値を求めようとするもので、解析の方もかなりの精度が要求されます。

　また、背景としては、現実の実験室モデルで、多くの電磁気的現象は解析的にも計算できますので、計算誤差は計算機の丸め誤差のみということもあります。　つまり、(物理現象の取り違えがないと考えて、)計算さえうまくやっておれば、合って当たり前の世界なのです。　このあたりが、他のCAEの分野とも若干、毛色の違うところでもあります。

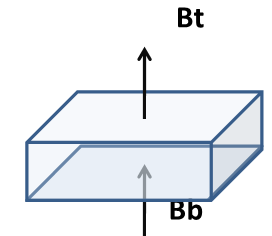
力に換算すると誤差が大きくなる例

　磁場応力は磁場の二乗に比例し、合力はその差になります。 つまり、1面に於ける磁束密度の結果から応力計算すると有効数字が極端に少なくなります。　マックスウェルの応力は

上部磁場: \(\mathbf{B_t} = 100±5\)　　上部応力: \(\mathbf{F_t} = c* (10000 ± 707.106)\)
下部磁場: \(\mathbf{B_b} = 105±5\)　　下部応力: \(\mathbf{F_b} = c*(11025 ± 742.462)\)

合力: \(\mathbf{F_b}-\mathbf{F_t}\)
= c(11025 – 10000) ± \(\sqrt{742.462^2 + 707.106^2}\)
= c(1025 ± 1025.304)

磁束密度の誤差が5%でも、力に換算すると誤差は100%･･･ということになってしまいました。

解析すべき現象の把握

　従いまして、解析すべき現象を把握して、次に述べる磁場解析の分類にかけ、どこで妥協できるのか判断することが重要です。　 解析目的にかなった、適切な選択こそが成功への秘訣です。　次章以降の、分類等をご参考になりご自身が抱えている問題解決の糸口として下さい。

シミュレーションモデルの次元

ジオメトリによる区分

　解析対象空間の次元または座標系

1. ０次元解析・・・空間的広がりは考えない。いわゆる集中定数系。一点モデルなどとよく言われます。
2. １次元解析・・・球対称として解く問題
3. ２次元解析・・・直交系((x, y):z方向は無限長)または円筒系(r, z)として解く問題
4. ３次元解析・・・直交系(x, y, z)、極座標系(r, θ, z)、または、自然座標系として解く問題

　次元レベルが高いほど、いろいろな効果・現象を精度良く解析できるのは当たり前ですが(２次元より３次元、３次元静解析より３次元動解析、線形解析より非線形解析)、取り扱う変数の数が幾何級数的に増えますので、関心のある問題の解の精度が得られるようにモデルを選択する必要に迫られます

　よく行われる方法として、解くべき問題の時空の対称性を考慮に入れて次元を減らし、問題を解きやすくする方法がとられます。 　例えば、高さ(z)方向に電磁場の変化が少ない問題を、二次元(x,y)電磁場解析問題として解くという方法です。　

　しかし注意すべき事として、一般的に、次元が少ない方が変数の数が少ないので解きやすいと思われていますが、 電磁場問題はもともと三次元(本当は四元)問題なので次元を減らしたためにかえって不可解な項?が出てきて、 問題を複雑にすることもあります。

　０次元解析(集中定数系)は、主解析の補助として用いられることがあります。　磁場解析に於いては外部負荷回路や電源・電流回路がそれにあたります。　集中定数として、回路素子としてのコイルのインダクタンス、コンデンサのキャパシタンス、抵抗値などがあります。　また、高次元解析の応答特性をダイナミックな計算結果として、伝達関数や状態方程式を組み合わせたものに0次元解析問題として縮約することができれば、応用・利用範囲は広がるでしょう。

　※ゲームの例ですが、攻撃力・防御力・… などで複数のパラメータセットで表してしまうものは典型的な集中定数系(0次元)モデルです。　いくらグラフィックが3Dでも、ゲームパラメータが0次元というのは良くあります。　この場合、ゲームでは同じようなものがパターン壊れ方をします。　しかし、現実では、ものの壊れ方一つとっても同じ壊れ方がありません。

時間依存性による区分

1. 静解析
   時間項を考えない静電場・静磁場解析。　モデルが動く場合でも、注目すべき現象の動解析で掲げる時間依存項が無視できる場合は、静解析でも十分です。　
   例　ステッピングモーター: 動くものでも瞬間・瞬間は写真で切り取ったような静解析の計算で構いません。
   
2. 動解析
   時間項を考慮した解析です。　動解析というと、モデルが動くことを想像しがちですが、実際にはそうではなく解析結果に時間依存項が大きく影響するかどうかが決定要因です。
   
   (1)モデルが動かないもの
   渦電流・逆起電力・変位電流・動電流(電場解析)など電磁場のみ動きに注目した狭義の動解析と
   
   (2)モデルが動いたり変形するもの
   モデルの動き・変形・(温度・力などの影響による)物性の時間的変化まで含めた広義の動解析があります。
   
   さらに、時間依存項が、定常のものと非定常ものとがあります。　これらは上記(1),(2)のレベルでもそれぞれ存在致します。
   
   (A)非定常解析
   過渡解析とも言います。　一過性の現象、あるいはランダムな現象を時間軸上で追ってシミュレーションする解析です。　大抵の場合は、解析のシナリオが存在します。　例えば、電磁機器の起動・停止などです。　もちろん、動く物が無くても電源投入時・切断時の場の変化を解析も含まれます。　非定常の時間項解析には、陽解法と陰解法がありますが、これについては後に詳しく述べましょう。
   
   (B)定常解析
   一定の周期で現象が繰り返されるものです。　いわゆる、”定常状態”の現象を解析するわけですが、”定常状態”と良く似たものとして、”平衡状態“というものがあります。　”平衡状態“は、外見上、物と場の変化が無いよう(マクロ的に時刻tに対して一定のバランスが保たれている)でも役者が入れ替わっています。　これを”定常状態”と呼ぶ場合もありますが、電磁場解析では”平衡状態”を解くのは定常解析ではなく、どちらというと静解析に分類されます。　(例　静磁場解析で一般的に扱う直流は一定の電流が流れているが、個々の電子は止まっている訳けではない。) 　つまり、定常解析では時刻tに対して周期的な変化をする場を求める解析ということになります。
   
3. 電磁流体解析
   
   　上で分類しました「1.動解析　(2)モデルが動いたり変形するもの」の特殊なものですが、さらに以下の二つに分かれます。
   
   (1)ミクロな視点で解くもの
   個々の磁性体・誘電体・導体(例えば鉄粉・イオン・コロイド粒子)などの状態を解くのもの
   
   (2)マクロな視点でとくもの
   集団としての挙動を扱おうとするものです。

物性による区分

　物性による区分をシミュレーションモデルの次元に入れたのは、かなり違和感を感じるかも知れませんが、実際に解析するという立場からすると、計算の過程で時空(x, y, z, t)を含めたループにさらに、もう一つ以上のループ(x, y, z, t, m, …)が加わる様相を呈することになるからです。

　物性による区分は複雑です。　電磁場の特性を決定づけるミクロ的な物性モデルは多次元関数または複雑なテンソル量になってしまいます。　 工業的応用範囲での電磁石・永久磁石等の感覚で、マクロ的な取り扱いのときにいかに簡単に(次元・次数を落とす等して)して扱うかがポイントとなります。 　(最近ではミクロ的な振る舞いまで考慮すべき工業製品も身の回りにあります。)

　言いかえれば、問題とされる解の精度・特性・領域(範囲)をできるだけ絞り込み、 それに必要な物性のみを取り扱うようにしなければなりません。　

　今日では、コンピュータの発達により、いわゆるフルオプションによる計算が安易に選択されますが、 あまりにも複雑過ぎる物性モデルは時間とお金の浪費です。　たとえできたとしても、自己満足にしか過ぎません。

　これは、ジオメトリや時間依存性の次元の取り扱いにも通じるところがあります。　 しかし、ジオメトリや時間依存性に関しては、可視的で比較的最適に近い選択を可能にしますが、 物性に関しては予見し難い面が多く見受けられます。　 それは、ジオメトリや時間依存性の次元を構成する変数の独立性があり、偏微分で見ると比較的線形的に変化するのに対して、物性の方は独立性ある変数を分離すること自体が難しいのです。　独立変数のループの場合、単純な多重ループでしかも、その規模は離散化数の乗算で見積もることができます。　しかし、複雑な依存性のあるもの、あるいはその状況が把握できないものには、再帰的なロジックによる収束計算が必要なことが、間々あります。　しかし、離散化の刻みが十分精度がないと、条件が満足することが保証できません。　したがって、解を得たときに必要条件の充足だけではなく、検証を行い、十分条件であるか検討することが不可欠です。

1. 線形解析
   
   取り扱う物性に直接的・間接的に電磁場依存性がない場合に用いることができます。　
   強磁性体を扱う磁場解析は一般に非線形です。
   線形解析を行うものに次のような例があります。
   
   1. 導体のみの動磁場解析(超伝導体の解析も含む)
   2. 導体のみまたは一般の誘電体の静電場解析　
   3. 電磁波解析
   4. 比較的影響の少ない間接的非線形
      線形解析では時間のかかる収束計算等が必要ないので、比較的メッシュ数の多い大規模なモデルまで取り扱えます。 　定常入力(交流等)の時間項に関して、複素数を利用して解くことができます。
      
2. 非線形解析
   
   　非線形性も直接的なものと間接的作用あるいは連成・連動計算の結果、非線形性を有するものがあります。 ここでは、直接的つまり電磁場解析だけで考慮しなければならない非線形性について分類してみます。 つまり、透磁率(誘電率)の磁場(電場)依存性ですが取り扱う次元により、
   
   1. 単にその強度のみに依存するとして取り扱う場合
   2. 方向依存性も考慮して取り扱う場合
   3. さらにヒステリシスを考慮して取り扱う場合
      に分かれます。

　ここで注意がいるのは、ヒステリシスを考慮する場合は、方向依存性を抜きにして扱うことが難しい場合が多いこと。　つまり方向依存性を考慮した取り扱いをしないとヒステリシスを考慮した解析結果が芳しくないことなどが多く報告されています。　また、磁場の動解析では、磁気余効という比較的遅いヒステリシスの変化がありますので解析時間のスパンによっては、実測と比べて、再現性に関わってくるので考慮しなければならないでしょう。　

連成・連動解析

　解析システム(系)として電磁場解析だけでは、シミュレーションの解が得られないというものです。　狭義で考えますと　電磁場解析は動磁場解析と動電場解析の連成ですし、さらに細かく分ければ、動磁場解析は静磁場解析+渦電流解析+α　という考え方もできます。　(実際のソルバーロジックはこのように作ることができる)

　しかし、ここで言う連成・連動解析とは、運動力学・構造解析・流体解析・化学変化・素粒子原子核変動など異次元のモデルの解析も同時に解かないとシミュレーションできないというものを指しています。 言い換えれば、「物性による区分」で示した非線形解析の発展形の一種と見なすことができます。

　いずれにしても、連成・連動解析は時間項を含む解析であることには変わりをありません。

　また、同時に解くという言葉は、実は奥深いものがあり、

　(1)別々のソルバーで通信しながら解く( ロジック的には同時ではないが、同じ時間軸で解く)
　　　例　異なったアプリケーションを交互に実行する。　連成でなく連動です。

　(2)一つのソルバーで違う次元のものを解く、内容的に(1)と同じものは含まれない。　つまり、典型的なものとしては構造解析と磁場解析のマトリックスを一つにして解くもの(マトリックス錬成が)がピュアな錬成解析と言えるでしょう。

　もちろん、精度の点から言えば　連成 > 連動　です。　難しさから言うと　連成　>> 連動　なのでコストに見合った選択が必要です。　また、異次元の系が単純であれば0次元集中定数系として、単一マトリックス取り込んでしまうという手も有効です。　

マルチフィジックス?

　ただし、異なった物理現象を同じモデル、つまり同じメッシュ分割で解くというのは、効率の良いものではありません。　個々の物理現象でボトルネックの場所とそのスケールが一致することは希で、非線形性も強く出るので八方美人的(美人とまでいけばいいのですが・・・)なモデルでは虻蜂取らずとなります。　教育用ならいいかもしれませんが、モノ作りで解析までして最適な性能を追求しようという方には向いていないでしょう。　

　メッシュだけではなく非モデル化・モデル化の取捨選択から、同じ形でも外形寸法の取り方(たとえば、無視できない円形ホールを外接多角形にするのか、内接多角形にするのか、その中間か・・・)、その解析特有のモデルに対する条件の入れ方等々、各物理現象ごとに個別に対応しなければよい解は得られません。　また、本質的に複数の物理現象が絡むと、周期境界性・対称性が崩れやすくフルモデルで計算することも覚悟しなければなりません。

　残念ながら、2021年1月現在出回っているマルチフィジックスと称されるソフトウェアは、前節の分類から言うとほとんどが連動であり、本節の問題も残されたままです。

　また、苦労してマトリックス連成でモデルを作成しても、マトリックスの性質が非常に悪くなるのが問題となります。　マトリックスの性質が悪いとは、数学的に言い換えると「条件数」が大きくなることです。　マルチフィジックスにした場合、非対角項が大きく、しかも多く現れるため条件数は大きくなってしまいます。　mumpsや　pardiso を使っての大規模並列のシミュレーションがありますが、とにかく大変です。

AIとの連携で進めた方がよい

　マルチフィジックスが要求されるような問題は、より現実解を求めていて、自動制御の判断として利用したいことが多いことと思います。　複数の物理現象をシミュレーションするソフトウェアを直接、合体させたり、連携させたりして、硬直した複雑な構成するのではなく、個別に信頼の置けるソルバーを用意して、AIの判断を利用し、より柔軟に現実解が得られるようにするべきでしょう。　ソフトウェアのコントロールも含めAIに任せることができる技術が望まれます。　また、いかに沢山のデータを集めても、結果を見て人間が判断するのはAIではなく単なる確率・統計学です。　今、ブレーキを踏むかアクセルを踏むか両方は同時にできないのだから、それを判断させて初めてAIと言えます。

電磁場解析法の種類

電磁場解析法の種類

　電磁場問題を解くことを広く電磁場解析法ということにしますと、その方法はいろいろあります。　もちろん問題を解くのに実験まで含めて言うのは少し範囲を拡げすぎですが、 現実問題を解くには、実験結果も利用することも含めて考えねばなりません。　解析=計算ということで、計算により実験を再現するというのが解析の最終的な目的であると思いがちですが、 工学としての目的は物を制御することにあるので、実験結果の再現だけでは不十分であったりします。　また、この場合、すべての解析が困難な場合は実験との併用で目的を達成したりすることがあります。　

　電磁場解析法に於いてはマックスウェルの方程式が原点なのですが、それ以外のいわゆる経験式(Empirical Formula)を利用することもあります。 　特に物性に於いては経験式は欠かせないでしょう。　というか物性の部分は経験式がほとんど・・・かな。　解析は(モンテカルロ法などを使わない限り)実験と違って、いわゆる計算誤差以外の統計学的誤差はありません。 実験値との差を理論誤差という場合がありますが、元々解く問題を近似したり、物理現象を省略、仮定したのだから、 近似による差あるいは理論による食い違いというべきでしょう。　もちろん、比較するとき実験値の方の実験誤差は考慮しなければなりません。

理論解析法

　理論解析値(Theoretial Analysis Value)を求める方法です。 理論解析値は、理論式から直接的・間接的に求めます。 　計算にコンピュータを利用するしても、電卓的利用から、エクセルやプログラムを利用して複雑な積分値の計算までするものもあります。 　次節以降のシミュレーションと大きく違うのは、初期段階に於いてモデルの離散化というものが無い点です。　空間的には理想的な形状を仮定したり、物性値の分布に平均値的なモノを利用・・・いわゆる集中定数系(0次元:一点モデル)として扱うことが多いのが特長です。 　コンピュータによるシミュレーションができなかった時代には、様々な経験式とともに、様々な理論が現実のモデルの近似値として扱われていまいした。　今でも、電気回路と伴に磁場解析を行う場合に利用されます。　　例として以下のような解析法があります。

• 複素数を利用した等角写像
• 磁気回路法
• パーミアンス法

微分方程式法

　コンピュータでシミュレーションとして汎用的な電磁界解析する場合は、マックスウェルの方程式から出発し、それに様々な離散化手法を駆使し、現実問題を解くものです。　離散化の過程でマックスウェルの方程式の微分的表現から出発したものを微分方程式法と呼ばれます。　　

微分方程式法

　コンピュータでシミュレーションとして汎用的な電磁界解析する場合は、マックスウェルの方程式から出発し、それに様々な離散化手法を駆使し、現実問題を解くものです。　離散化の過程でマックスウェルの方程式の微分的表現から出発したものを微分方程式法と呼ばれます。　　

有限要素法(FEM)

　微分方程式法の代表格です。　有限要素法は、世界的に学会および産業界でも広く研究・利用され多くの論文や理論が発表されています。　中でも辺要素有限要素法は優れた手法で、市販のプログラムにも採用され多くの実績を実らせています。

積分方程式法

境界要素法(BEM)

　モデルの表面のみ分割する方法です。　メッシュ分割は簡単で、計算も速いのですが、モデル内部に湧き出し・消滅がある問題は解くことができません。　 つまり、同じ物性でも解となる場の関数になるような非線形性がある場合、内部に湧き出し・消滅がありますので適用できないと考えてください。 ただし、積分法ですので重ねあわせがきき、局部的なモデルの解法として利用することができます。　電磁場解析の場合、強磁性体は一般的に B-H曲線を持った非線形性を有しますので、BEMだけで解くのはかなりの近似といえましょう。　それに対して、静電場解析のようなものは、 導体と誘電体(ほとんど非線形性がない)だけですので、かなり有効的に利用できます。

磁気モーメント法(IEM)

　BEMの欠点である非線形性を考慮するため、モデル内部までメッシュ分割する方法です。　弊社ソルバーQmがこの手法に該当します。　 BEMの場合もそうでなのですが、この方法を成功させるには、積分を精度よく、効率良く行う必要があります。　磁気モーメントという呼び名は 磁石などの磁性を示す単純なベクトル的イメージがどうしてもまとい付くのですが、実際の磁性体は細かい磁区が分布しているのであるので そのことを良く考えて、計算モデルを作成する必要があります。　また、渦電流解析は双対原理を使えば(※渦を双極子と考えると磁気双極子の計算はまさしく磁気モーメント法である)、 この手法と統一的に取り扱うことができます。 弊社のQmではこれによって動磁場解析を可能にしました。

感度解析

逆解析

　これまで述べた解析法はいずれも、いわゆる正解析(Forward計算)つまり、ソースから場を計算する手法でした。　それに対して、特定の場あるいは評価値(レシーバ)から、ソース分布 を求めるという逆解析を求めたいときもあります。　方程式としては、随伴方程式(Ajoint Solution)というものになります。 最適設計には必ず現れる考え方です。　具体的には 荷電粒子のビーム曲げる最適磁場を作る磁石の設計などがあります。

コントリビュートン

　まだ研究例が少ないのですが、ソースとレシーバが決まっているとき、ソースからレシーバへ流れの影響度を、位置の関数として表現することができます。　これを コントリビュートン(Contributon:Contributionではないので注意)といい、小磁性体の位置決定などに使えそうです。　筆者は地雷探査などに利用できるのではないかと考えています。　
参考: Contributon to Modeling of Coronal Magnetic Field

番外　テクノロジーの最終目標?…可制御と役立ち論

　※この項目は私個人の戯れ言ですので、読まれる方はご注意下さい。

テクノロジーの最終目標

　私は、テクノロジーの最終目標はモノ(物体・物質・エネルギー)の可制御だと考えています。 これに対して、作った(プログラム等も含め) モノの役立ち論を展開する人がいますが、そのテクノロジーが役に立つかどうかはかなり主観的です。 　つまり、役に立つかどうかは、利用側の事情・利用者の能力や主観によって変わってくるものです。 　例えば、山奥にコンセントが必要な電気製品を持っていって、役に立たないから電気製品の技術を否定することに似ています。

役に立つかどうかは使う側の問題

　つまり、どんなに優れたテクノロジーであっても、利用者の能力が無かったりなども含めて、利用する環境が整っていなければ役に立たないのです。　俗に言う猫に小判の状態です。・・・これがとても多い。 　優秀な部下をうまく使えないどこかの上司とよく似ていますね。 　それを、役に立たないからといって、そのテクノロジー自体を否定するのは筋違いと言えるでしょう。　　そのとき役に立たないと思っていたことが後で、とんでもなく役に立つことがあります。

　未来のこと、あるいは、見えている範囲外を100%予測することは不可能ですから、それが役に立つかどうか、 当事者だけで考えてモノを開発するのは、物事の一面しか見ていない偏った見方と言え、後に大きな禍や利益を損なうことになり得ます。 　そのとき役に立たなくても、可制御であれば、後に誰かがそれを利用しようと思ったとき役に立つことができるからです。　しかし、そのことは誰も予測不可能な場合が多いのです。 　つまり、役立ち論は「結果論で主観的なものである」ということを肝に銘じておいた方がよさそうです。 　ですから、可制御までがテクノロジーの最終目標とした方が、より普遍的な見方といえます。

モノ作りの目標と混同しないこと

　ここで、私の主張を誤解してもらっては困るのですが・・・、上記はテクノロジーの最終目標であって、実際のモノ作りの目標ではありません。 　モノ利用する側から見た作る目的(役立たせるかどうかは別)を曖昧にしていいと言っているのではありません。 　作る動機はまさに、その主観・役立ちから発せられるものです。 　ソフトウェアに限ったことではないのですが、設計段階では「要求定義」をできるだけ具体的にはっきり決めておねばなりません。 　

要求定義は非常に重要

「要求定義」は非常に大事です。 　これを決めておかなかったり、決めていても利用者と制作者でコンセンサスがとれていなかったりすると必ず大きなトラブルに発展します。 　「要求定義」は後に変更されることはあります。　ですから、尚更、はっきり決めておく必要があります。 　この世では、開発したモノが利用されなければ広まらないことも事実ですから、本来の目的とする機能は満たされることはもちろんのこと、人間工学的に使いやすい、便利なものを作るべきであるのはいうまでもありません。 　「要求定義」や「設計」の変更は、その制作過程で、その「利便性」に問題が生じたとき行われることが多いのです。(目的とする機能まで変えるのは変更ではありません・・・作り直しです。)　特にソフトウェアは「人間工学的に使いやすい」ということが重要ですね。　今のGUIやウィンドウシステムもそれが目的で巨費を投じて作られてきましたから・・・

設計上の欠陥は避けたいがオーバースペックはほどほどに

　「要求定義」を満たせば、役立つはずです。　作ったのに役に立たないのは、要求定義を満たしていないのか、要求定義が曖昧とかで欠陥があったからです。　言い換えれば、前者は、製造過程での欠陥で、後者は、要求定義自体の精度が品質に影響した設計段階での欠陥ということです。　勢い「可制御」である範囲を拡げれば(オーバースペックなど)要求を満たしやすいのですが、これも、本末転倒で、要求定義の作り直しから始めないと泥沼にはまります。

諭吉の言う実学とは

　一般的に学問的研究の目的を言う場合、前者のテクノロジーの最終目的を指すことが多いようです。　 それに対して、一般社会の技術利用の目的は後者の モノ作りの目標になっていると思います。　私は工学部出身ですが、 工学部は理学部と違い役に立つものを研究しなければならない・・・とよく言われました。 福沢諭吉さんが言う実学のことを指しているのだと思いますが、しかし、どこかで、 引っかかるものを感じていました。　諭吉さんの時代は富国強兵策でしたので その背景が色濃かっただと思います。　それは、
(1)学問的研究(=真理の探究)
(2)技術の目標(=可制御)
(3)モノ作りの目標(=要求定義を満たすこと)
が混じっていたからでしょう。　これらの境界を明確にして研究・開発している人は少なく、特に大学の工学部は(2)と(3)がごちゃごちゃになっているように思います。　企業の研究・開発はほとんどの場合、明確な要求定義を持っており、ほぼ(3)ですね。　産学連携のとき、このあたりが明確でないと(少なくとも当事者の立場が明確でないと)トラブルの元になります。

SFの永遠のテーマ

　これらのジレンマは、SF映画などにも良く根底のテーマとしてもよく使われていると思います。　時代にそぐわない優れたテクノロジーが 研究者の思いもつかぬものに利用(悪用)されて、悲劇を招くという筋書きです。

　前者を科学(理論・研究)と後者を技術(利用・応用)という構図で考えてみましたが、あまりにも身近な言葉なので、 その意味は余計にわからなくなります。　両者は、対立するものでもなくむしろ親和性が高いもので、互いに助け合って進歩してきたものですから、普段は混同しても差し支えないのですが、ここぞと言うときには 違いをはっきり区別しておくべきでしょう。　特に、今流行の役立ち論は「結果論で主観的なものである」ということを・・・くれぐれもご都合主義に流されないよう注意いたしましょう。

　希に、誰もが役立たないと思ってしたモノに、優れた利用方法を見つける賢人がいますが、このような人は特別で、私を含めた凡人はコツコツと目の前の身近な目標に向かって進むしかないです。