2021年11月11日 / 最終更新日時 : 2022年10月2日 ichida@slock.co.jp 技術情報

時系列関数の記述法

1 はじめに
2 時系列関数の生成
3 ジェネレータ系関数
4 数学系基本関数
5 スイッチング系関数
6 出力系関数

はじめに

ここでは「Qm」の動磁場の機能で特長のあるものついて、ほんの一部ですがご紹介いたします。　
応用例として「方形波電源のLR, CR回路の過渡応答の例」もご参照下さい。

時系列関数の生成

動磁場解析では時系列データが出力されます。時系列データの候補としては、電流・電圧・磁場・座標・速度。加速度等の時々刻々変化があります。　これらは、出力だけではなく、外部入力条件としても与えたい場合もあります。つまり、動磁場解析では入力データに関しても時系列データをうまく取り扱わねばなりません。

単純な変化の場合は、タイムステップごとに入力できるでしょうが、少し複雑な変化になると、データ作成手間が大変です。　また、エクセル等でソルバー外部でデータを作成していると、ソルバー側のタイムステップ幅の変えた場合、 再サンプリングの必要があるのですが、うっかり間違ってしまうことがあります。 間違いなく、複雑な条件を入れるためには、ソルバー自体に汎用的な関数発生や合成のメカニズムが必要です。

　Qmでは、これらを解決するため、制御・数学等でよく用いられる関数を多数用意し、それらを四則演算・合成できる機能を持っています。

用意された関数を以下に紹介いたします。

関数群は機能別に、

ジェネレータ系関数　… 制御工学で使う基本的な関数
数学系基本関数　　… 数学で使う関数。　関数電卓にあるものが中心。
スイッチング系関数 …　他の関数と接続することにより、条件回路が組める関数。
出力系関数 …　計算結果をフィードバックさせるために使用する関数。

があります。

もちろん、これらの関数の事前プロット・サンプリングの様子を含めたグラフ作成機能もあります。

「時系列関数」は、最終的に時間を独立変数とするのスカラー関数　F(t)　として与えます。　「時系列関数」は、「一様磁場」(MConstField)・「強制電流」(MForcedCurrent)そして、「運動」(MMotion)などのスカラーパラメータとして利用される汎用的な関数群です。　従いまして、「時系列関数データ」は単独で用いることはなく、常に他の「物性データ」や「解析条件」で引用するのに使用します。

１つの「時系列関数データ」は、複数の異なった「物性データ」や「解析条件」に使用可能です。　ただし、その「時系列関数データ」を変更すると、それを使用している「物性データ」や「解析条件」もすべて変更されます。

ジェネレータ系関数

ジェネレータ系関数は電流・電圧・速度・加速度などのソース(発生源)となるものが用意されています。以下にその関数の仕様を示します。

ジェネレータ系関数選択画面

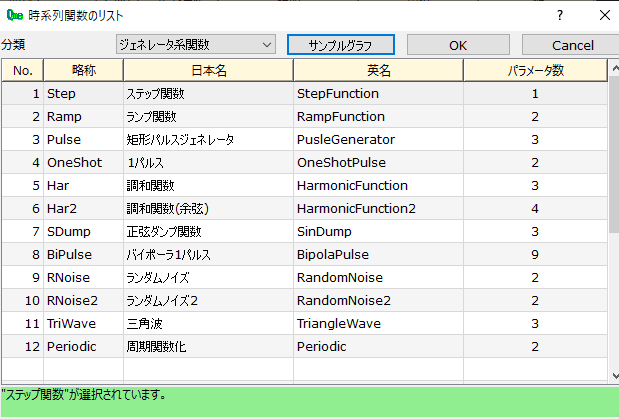
Qmでは、上記画面の「グラフ表示」のボタンを押せば、これから使う関数のサンプルプロット図が得られます。　下記関数表説明の図をクリックするとその拡大図が表示されます。　
実際のシミュレーションでは、Qmの別の画面でサンプリングプロット図見ながら、これらの関数を式で合成します。

ジェネレータ系関数表

ジェネレータ系関数

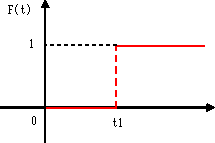
ステップ関数

t = t1 で　値が0から1に変化します。
ステップ関数の大きさは、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 1個

No.

記号

既定値

説明

StepFunction
(Step)

F(t)=0	: t＜t1
F(t)=1	: t1≦t

0.0

遅延時間

ジェネレータ系関数

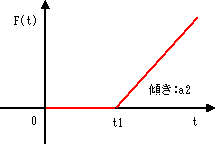
ランプ関数

t=t1 で　値が0から直線的に増大します。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

RampFunction
(Ramp)

F(t)=0	: t＜t1
F(t)=a2・(t-t1)	: t1≦t

0.0

遅延時間

1.0

傾き

ジェネレータ系関数

矩形パルスジェネレータ

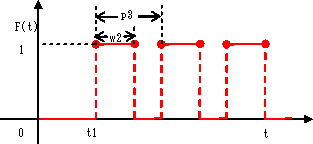
t=t1 から指定幅の矩形パルスを一定周期で発生させます。
パルス高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Pulse
Generator
(Pusle)

F(t)=0	:		t＜t1
F(t)=1	: t1+p3・i	≦	t＜t1+p3・i+w2
F(t)=0	: t1+p3・i+w2	＜	t＜t1+p3・(i+1)
	i = 0, 1, 2, …

0.0

遅延時間

1.0

パルス幅

2.0

周期

ジェネレータ系関数

1パルス

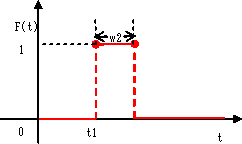
t = t1 から指定幅の矩形パルスを一つ発生させます。
パルス高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

OneShotPulse
(OneShot)

F(t)=0	:		t	＜ t1
F(t)=1	: t1	≦	t	≦ t1 + w2
F(t)=0	: t1 + w2	＜	t

0.0

遅延時間

1.0

パルス幅

ジェネレータ系関数

調和関数

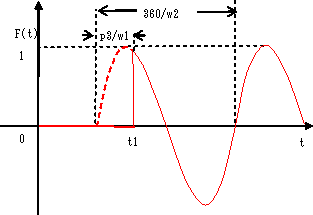
t = t1 から周期　360/w2 のsin波を発生させます。
正弦波ですが数学関数系とはパラメータの構成が異なります。
波高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

HarmonicFunction
(Har)

F(t)=0	:	t ＜t1
F(t)=sin(w2・(t – t1)　+ p3)	:t1 ≦	t

0.0

遅延時間

1.0

角速度

2.0

位相

ジェネレータ系関数

調和関数(余弦)

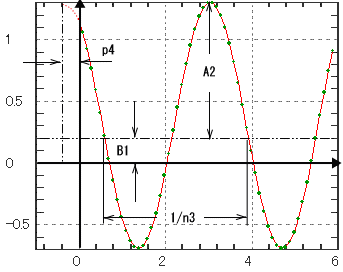
t =0 からバイアス値B1 振幅A2　振動数n3 位相角p4 のcos波を発生させます。
余弦波ですが数学関数系とはパラメータの構成が異なります。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

HarmonicFunction2
(Har2)

F(t)=A2・cos（360・t・n3 + p4 ）+ B1

0.0

バイアス値

1.0

振幅

60.0

振動数

0.0

位相角

ジェネレータ系関数

正弦ダンプ関数

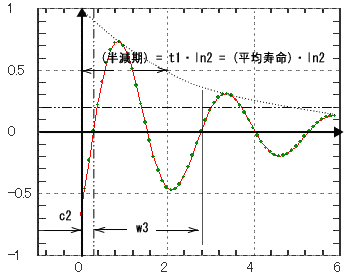
t = 0 から周期　360/w2 のexp(-t/t1)で減衰するsin波を発生させます。
波高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

SinDump
(SDump)

F(t)=exp(-t / t1)・sin(180・((t　-　c2)　/　w3))

1.0

平均寿命

1.0

中心

1.0

周期

ジェネレータ系関数

バイポーラ1パルス(台形波)

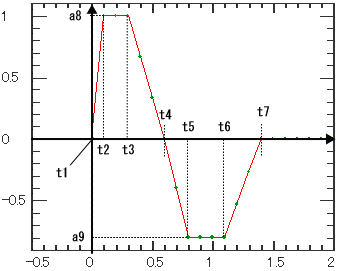
t = t1 から指定幅のバイポーラパルスを一つ発生させます。
t1～t7まで屈折する時刻を与えます。
パルス高は、a8, a9 のパラメータで与えます。
周期関数化したいときは後述の周期関数ジェネレータを使用します。

関数名

式

パラメータ 9個

No.

記号

既定値

説明

BipolaPulse
(BiPulse)

F(t)=0	:		t ＜ t1
F(t)=a8・(t – t1)　/ (t2 – t1)	:	t1 ≦	t ＜ t2
F(t)=a8		t2 ≦	t ＜ t3
F(t)=a8・(t – t3)　/ (t4 – t3)		t3 ≦	t ＜ t4
F(t)=a9・(t – t4)　/ (t5 – t4)		t4 ≦	t ＜ t5
F(t)=a9		t5 ≦	t ＜ t6
F(t)=a9・(t – t6)　/ (t7 – t6)		t6 ≦	t ＜ t7
F(t)=0		t7 ≦	t

0.0

上昇開始時刻

0.1

頂点到達時刻

0.3

下降開始時刻

0.6

0点通過時刻

0.8

底辺到達時刻

1.1

再上昇開始時刻

1.4

終了時刻

1.0

パルス頂

-0.8

パルス底

ジェネレータ系関数

ランダムノイズ

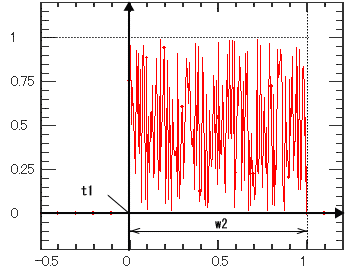
t = t1 からランダムノイズを発生させます。サンプリングごとに0＜ξ＜1の一様乱数が発生します。　
従いまして、変化は1/Δtで生じます。波高は、dFuncFactorキーワードで与えてください。
▼乱数発生は順序は、Qmeのシミュレーションだけではなく、サンプル時の表示も含めての他所も通じて呼び
出した回数で決まりますので再現性は保証されません。
▼ランダムに時間的に変化する一様変動磁場では、この関数ではなく、ランダムノイズ2を使用して下さい。
この関数を使用してはいけません。一様磁場の計算では、同じタイムステップで、複数回異なった位置での
呼びだしを行うため、呼びだし毎に異なった値を返すからです。　つまり、その結果、同時刻で空間的に一様
でない値を発生させるからです。　

関数名

式

パラメータ 2個

No.

記号

既定値

説明

RandomNoise
(RNoise)

F(t)=0	:		t	＜ t1
F(t)=ξ	: t1	≦	t	≦ t1 + w2
F(t)=0	: t1 + w2	＜	t

0.0

遅延時間

1.0

発生時間

ジェネレータ系関数

ランダムノイズ2

t = t1 からランダムノイズを発生させます。 0＜ξ＜1の一様乱数が発生します。　
同じタイムステップ・同じデータIDで、同じ値を返します。従いまして、変化はデータIDが違うとき及びタイムステップ
が異なるときのみ生じます。また、計算前のグラフ表示では乱数を発生させることができないので、計算前
は恒常的に値1を返します。
波高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

RandomNoise
(RNoise2)

F(t)=0	:		t	＜ t1
F(t)=ξ	: t1	≦	t	≦ t1 + w2
F(t)=0	: t1 + w2	＜	t

0.0

遅延時間

1.0

発生時間

ジェネレータ系関数

三角波

t = t1 から周期p3の三角波を発生させます。 r2はp3=2 としたときに0≦r2≦1で頂点の位置を示します。
r2 ＜0　のときは　r2 = 0 とみなし、1＜r2　のときはr2 = 1 とみなした鋸波となります。
波高は、dFuncFactorキーワードで与えてください。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Triangle
Wave
(TriWave)

F(t)=0	:		t	＜ t1
以下はp3=2としたときの各周期での波形
F(t)=(1/r2)(t-t1)	:t1	≦	t	＜t1+r2
F(t)=1-2/(2-2r2)(t-t1–r2)	:t1 + r2	≦	t	＜p3–r2=2-r2
F(t)=(1/r2)(t-t1-(2-r2))-1	:p3-r2=2-r2	≦	t	＜p3 = 2

0.0

遅延時間

0.5

ピーク位置

2.0

周期

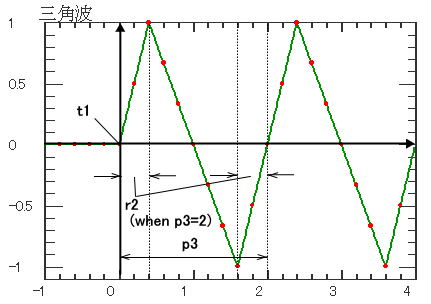r2の値は周期内での鋸の歯の頂点の位置を示します。p3 = 2 のとき、r2 = 0, r2 = 0.5, r2 = 1の時の波形を下図に示します。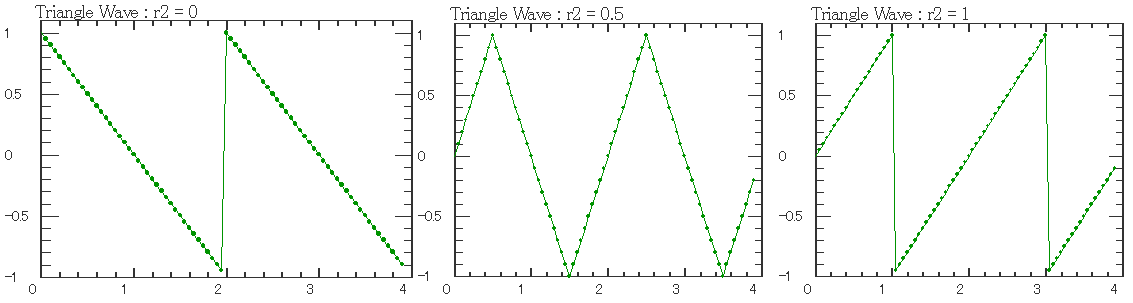

ジェネレータ系関数

周期時間ジェネレータ

t = t1 から周期p2の時間を発生させます。この関数を時間軸として使用すると、単発の波形も周期関数となります。
▼Periodicという名ですがノコギリ波の一種です。
他の関数を周期化するには、Periodicを、独立変数t(時間)に代わるものとして使用します。
g(t) = OneShotPulse(t) に対して
g(t) = OneShotPulse(Periodic(t)) とすればパルスジェネレータとなります。
▼g(t) = Periodic(OneShotPulse(t))　ではありませんのでご注意。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Periodic

F(t)=0	:		t	＜ t1
F(t)=(t-t1) % p2	:t1+ p2・i	≦	t	＜ t1 + p2・(i + 1)
	i = 0, 1, 2, …

ち

0.0

遅延時間

1.0

周期

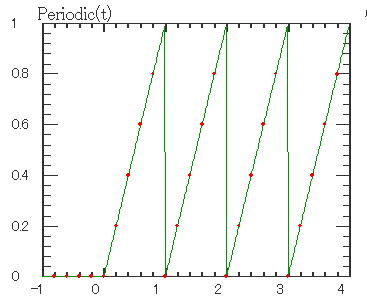時間軸として使用する例は以下のとおりです。
[Dat
sKind = MTimeFunction
nID = 1
psFunction = Periodic
sOperator = T
dParams = 0 2
psFunction = BipolaPulse
sOperator = +
dParams = 0 0.1 0.3 0.6 0.8 1.1 1.4 1 -0.8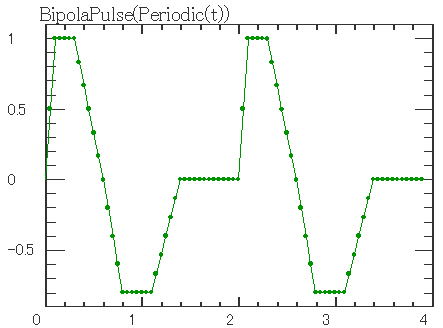
]

数学系基本関数

数学系基本関数は関数電卓で使用する基本的な関数が用意されています。　これらの関数の四則演算記述することができますが、なるべく簡単な入力で複雑な式を入力できるように、多くの関数はそれ自身のパラメータとして、オフセットと大きさを持っています。

数学系基本系関数選択画面

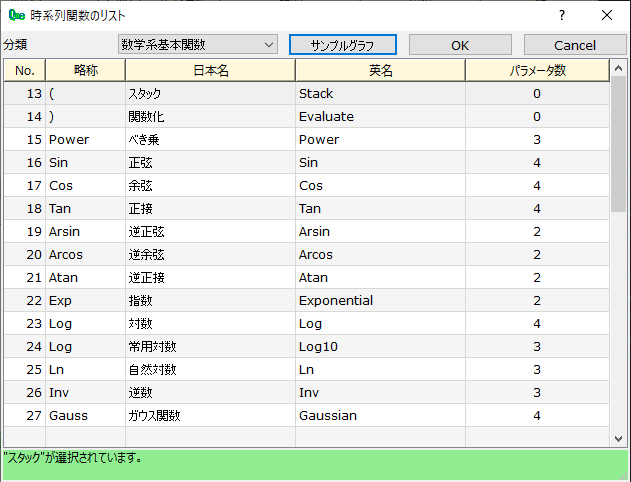
数学系基本関数表

関数名	式	パラメータ入力順に0,1.. 番号添付
関数名	式	記号	既定値	説明
Stack (	(…	なし		新たな式を始めます。　それまでの式はスタックされます。(push)　開き括弧のような効果があります。
Evaluate )	…)	なし		四則演算結果を評価し関数化します。直前に四則演算の結果が必要です。　閉じ括弧のような効果があります。　スタックがあれば引き出します。(pop)
Power	y = y1 + A2*tⁿ³	y1:オフセット A2:大きさ n3:べき乗	0 1 2	べき乗
Sin	y = y1 + A2sin(w3t+p4)	y1:オフセット A2:振幅 w3:角速度 p4:位相角	0 1 360 0	正弦
Cos	y = y1 + A2cos(w3t+p4)	y1:オフセット A2:振幅 w3:角速度 p4:位相角	0 1 360 0	余弦
Tan	y = y1 + A2tan(w3t+p4)	y1:オフセット A2:振幅 w3:角速度 p4:位相角	0 1 360 0	正接
Arsin	y = y1 + A2*arcsin(t)　: 　-1≦t≦1	y1:オフセット A2:大きさ	0 1	逆正弦 -1≦t≦1 の範囲外は鏡像対称の周期境界。
Arcos	y = y1 + A2*arccos(t) : 　-1≦t≦1	y1:オフセット A2: 大きさ	0 1	逆余弦 -1≦t≦1 の範囲外は鏡像対称の周期境界。
Atan	y = y1 + A2*arctan(t)	y1:オフセット A2: 大きさ	0 1	逆正接
Exponential Exp	y = y1 + A2*exp(t)	y1:オフセット A2: 大きさ	0 1	e指数
Log	y = y1 + A2*Log a3( t – t4 )	y1:オフセット A2 :大きさ a3 :底 t4:開始限界点	0 1 10 0	対数
Log10	y = y1 + A2*Log10 ( t – t3 )	y1:オフセット A2 :大きさ t3:開始限界点	0 1 0	常用対数
Ln	y = y1 + A2*Ln( t – t3 )	y1:オフセット A2:大きさ t3:開始限界点	0 1 0	自然対数
Inv	y = 1 /(A2*(t-t3)+ y1)	y1:逆オフセット A2:大きさ t3:	0 1 0	逆数
GaussianFunction Gaus	y = y1 + A2exp(-(t-c3)^2/(2w4^2))	y1:オフセット A2:振幅 c3:ピーク位置 w4:半値幅	0 1 0 1	ガウス関数

数学系基本関数　詳細

数学系基本関数

スタック

新たな式を始めます。　それまでの式はスタックされます。
(push)　開き括弧のような効果があります。
単独で使用することはできません。
先頭の開き括弧はデフォルトで設定されているので指定しません。
★この関数に付く演算子は意味を持ちません。

関数名

式

パラメータ 0個

No.

記号

既定値

説明

Stack
(

(…

–

数学系基本関数

関数化

四則演算結果を評価し関数化します。
直前に四則演算の結果が必要です。　
閉じ括弧のような効果があります。　
スタックがあれば引き出します。(pop)

関数名

式

パラメータ 0個

No.

記号

既定値

説明

Evaluate
)

…)

–

数学系基本関数

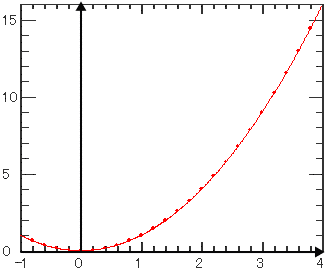
べき乗

時間(独立変数)のべき乗を計算します。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Power

F(t) = y1 + A2 * t　^p3

0.0

オフセット

1.0

大きさ

2.0

べき乗

数学系基本関数

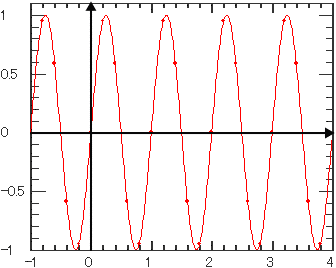
正弦

時間(独立変数)の正弦を計算します。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

Sin

F(t) = y1 + A2 * sin(w3 * t + p4)

0.0

オフセット

1.0

振幅

360.0

角速度

0.0

位相角

数学系基本関数

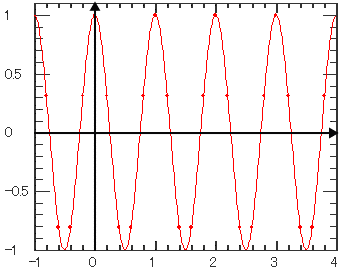
余弦

時間(独立変数)の余弦を計算します。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

Cos

F(t) = y1 + A2 * cos(w3 * t + p4)

0.0

オフセット

1.0

振幅

360.0

角速度

0.0

位相角

数学系基本関数

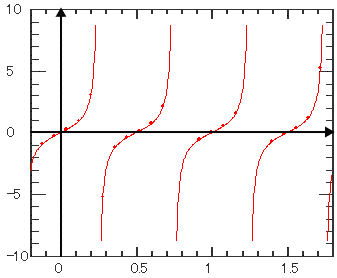
正接

時間(独立変数)の正接を計算します。
定義域を超えた場合はサイクリックに適用されます。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

Tan

F(t) = y1 + A2 * tan(w3 * t + p4)

0.0

オフセット

1.0

振幅

360.0

角速度

0.0

位相角

数学系基本関数

逆正弦

時間(独立変数)の逆正弦を計算します。
定義域を超えた場合は(関数の連続性を保つため)交互に反転しながらサイクリックに適用されます。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Arsin

F(t) = y1 + A2 * arcsin(t)

: -90≦arcsin(t) ≦90 :

0.0

オフセット

1.0

大きさ

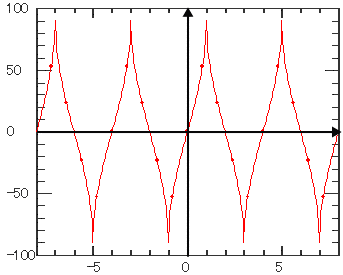数学系基本関数

逆余弦

時間(独立変数)の逆余弦を計算します。
定義域を超えた場合は(関数の連続性を保つため)交互に反転しながらサイクリックに適用されます。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Arcos

F(t) = y1 + A2 * arccos(t)

::0≦arccos(t)≦180

0.0

オフセット

1.0

大きさ

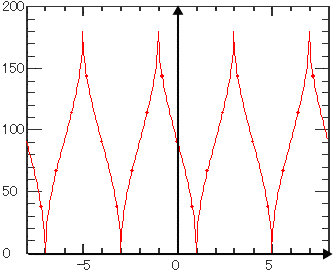数学系基本関数

逆正接

時間(独立変数)の逆正接を計算します。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Atan

F(t) = y1 + A2 * arctan(t)

: -90≦ arctan(t) ≦90

0.0

オフセット

1.0

大きさ

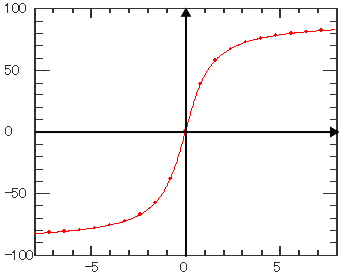数学系基本関数

e指数

時間(独立変数)のネピア数を底とする指数関数を計算します。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Exponetial
Exp

F(t) = y1 + A2 * exp(t)

0.0

オフセット

1.0

大きさ

数学系基本関数

対数

時間(独立変数)の対数を計算します。
開始限界点以下は0値を返します。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

Log

F(t) = 0	: t ≦ t4
F(t) = y1 + A2 * Log _a3(t – t4)	: t4 ＜ t

0.0

オフセット

1.0

大きさ

10.0

底

0.0

開始限界点

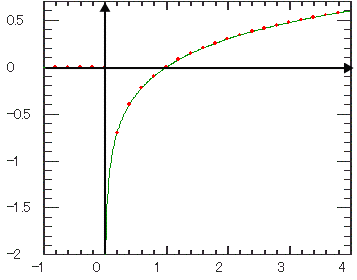数学系基本関数

常用対数

時間(独立変数)の常用対数を計算します。
開始限界点以下は0値を返します。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Log10

F(t) = 0	; t ≦ t3
:F(t) = y1 + A2 * Log(t – t3)	: t3 ＜t

0.0

オフセット

1.0

大きさ

0.0

開始限界点

数学系基本関数

自然対数

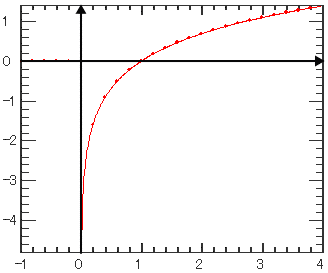
時間(独立変数)の自然対数を計算します。
開始限界点以下は0値を返します。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

F(t) = 0	; t ≦ t3
:F(t) = y1 + A2 * Ln(t – t3)	: t3 ＜t

0.0

オフセット

1.0

大きさ

0.0

開始限界点

数学系基本関数

逆数

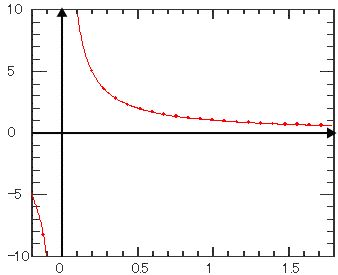
時間(独立変数)の逆数を計算します。
t = t3 では0値を返します。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Inv

F(t) = 0	: t ＝ t3
F(t) = y1 + 1/(A2 * (t – t3))	: t ≠ t3

0.0

y軸漸近線

1.0

大きさ

0.0

t軸漸近線

数学系基本関数

ガウス関数

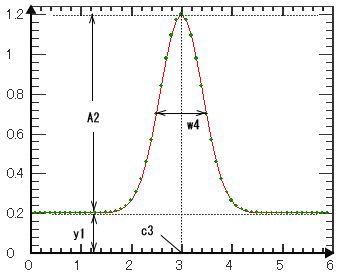
時間(独立変数)のガウス関数を計算します。
GCW はw4を半値幅に調整するための定数でGCW　= 4ln2 ≒2.7725887 です。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

Gaussian
Gauss

F(t) = y1 + A2 * exp( – GCW * (t – c3)^2 / ( w4^2))

0.0

オフセット

1.0

振幅

0.0

ピーク位置

1.0

半値幅

スイッチング系関数

「時系列関数」のスイッチング系関数は、状態変化による制御に用いられます。以下にその関数の仕様を示します。

スイッチング系関数は入力となる関数 x0, x1, … をDatIDで指定し、スイッチングします。　

ジェネレータ系関数・数学系関数との大きな違いは、時間軸t(独立)変数を持たないことです。　

従いまして、入力関数として他の関数と併用する必要があります。　

入力関数は、

(1)外部(他のDatIDを持つMTimeFunction) からを与える方法と、

(2)同じ時系列関数内で演算子として指定する方法があります。

(2)の方法では、sOperatorキーワード(演算子)で内部(同じDatIDのMTimeFunction)から入力関数を与えることとなりますが、演算子 T は入力関数 x0 に対応し、演算子 X1～X5 は、入力関数 x1～x5 に対応します。このとき入力関数が与えられた x1～x5 の DatIDは　0 にして下さい。

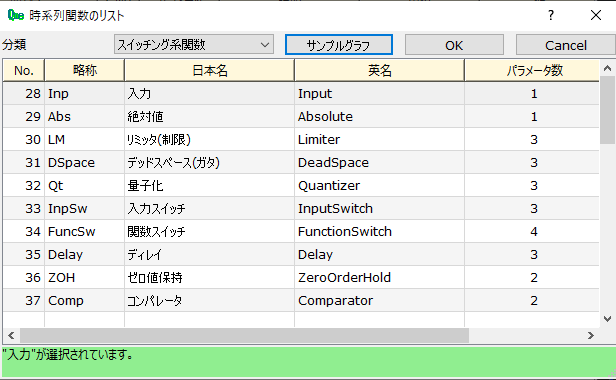
スイッチング系関数表

スイッチング系関数

入力

DatIDの関数値をそのまま出力します。他で定義した任意の関数をDatIDで参照するときに使います。

関数名

式

パラメータ 1個

No.

記号

既定値

説明

Input
Inp

F(x1) = x1(t)

入力関数のDatID

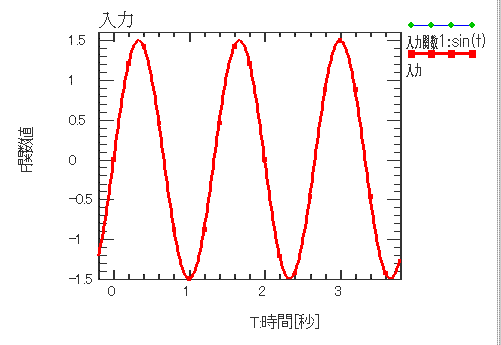入力関数　X1(t) = sin(t)　としたとき、 Input関数(入力)の出力が　F(t) = Input(X1(t))　となり
入力と完全に一致していることを示しています。

例えば、DatID = 3の関数結果とDatID = 4の関数結果の和(四則演算など)を求めたいときなど
に使用します。

スイッチング系関数

絶対値

入力関数の絶対値です。

関数名

式

パラメータ 1個

No.

記号

既定値

説明

Absolute
Abs

F(x1) = |x1(t)|

入力関数のDatID

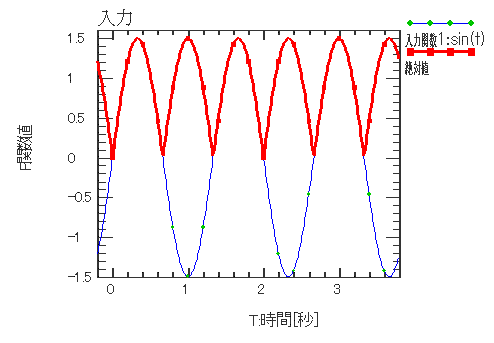入力関数　X1(t) = sint(t)
絶対値　F(t) = Abs(X1(t))

スイッチング系関数

リミッタ(制限)

関数値の上下値を制限します。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Limiter
LM

F(x1) = min2	: x1(t) ＜ min2
F(x1) = x1(t)	: min2≦ x1(t)≦max3
F(x1) = max3	: max3 ＜ x1(t)

入力関数のDatID

min2

-1.0

有効開始点

max3

1.0

有効終了点

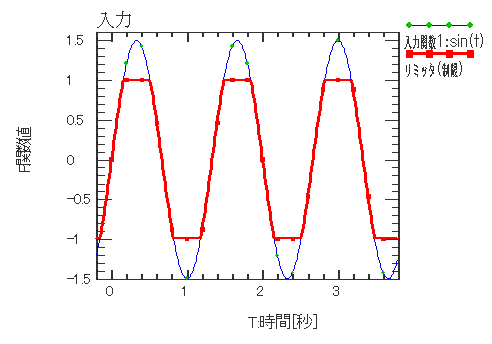入力関数　X1(t) = sint(t)
リミッタ　F(t) = Limiter(X1(t))

スイッチング系関数

デッドスペース(ガタ)

指定範囲内の変化は吸収され出力されません。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

DeadSpace
DSpace

F(x1) = x1(t)-min2	: x1(t) ＜ min2
F(x1) = 0	: min2≦ x1(t)≦max3
F(x1) = x1(t)-max3	: max3 ＜ x1(t)

入力関数のDatID

min2

-1.0

不感開始点

max3

1.0

不感終了点

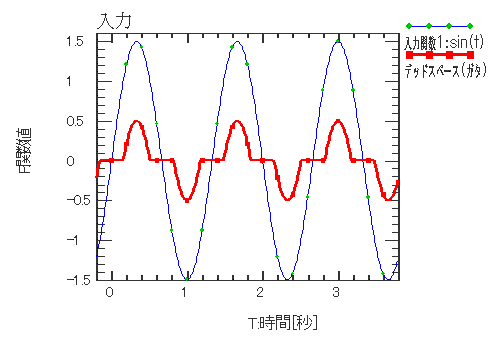入力関数　X1(t) = sint(t)
デッドスペース　F(t) = DeadSpace(X1(t))

スイッチング系関数

量子化

量子化(Quantizer)　量子化は、入力関数x1(t)を一定の段差w2の階段状関数に変換します。
d3=0は階段関数が下から接し(入力関数を超えない)、
d3=1は上から接し(入力関数を下回らない)、
d3=0.5は中央値をとります。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Quantizer
Qt

F(x1)= [x1(t)/w2 + d3]*|w2|

[　]はガウス記号

入力関数のDatID

1.0

量子化幅

0.5

切上割合

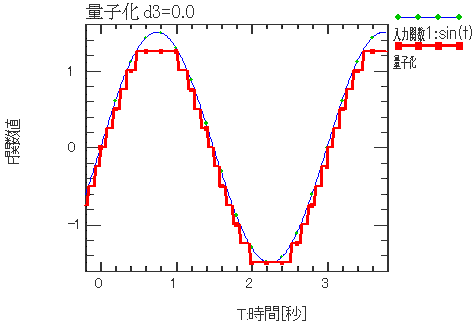入力関数　X1(t) = sint(t)
量子化　F(t) = Quantizer(X1(t), 1, 0.0)

入力関数　X1(t) = sint(t)
量子化　F(t) = Quantizer(X1(t), 1, 0.5)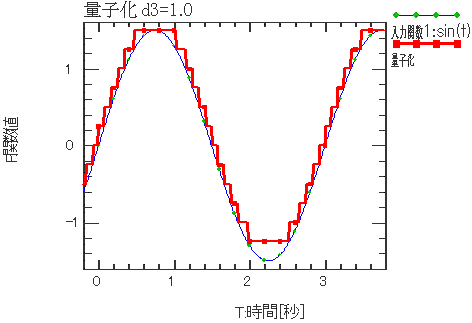

入力関数　X1(t) = sint(t)
量子化　F(t) = Quantizer(X1(t), 1, 1.0)

スイッチング系関数

入力スイッチ

2つの入力関数をスイッチ用入力関数の正負によってスイッチングします。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

InputSwitch
InpSw

F(x1,x2,x3) = x2(t)	: x1(t) ≦ 0
F(x1,x2,x3) = x3(t)	: 0 ＜ x1(t)

スイッチ用入力関数のDatID

入力関数1のDatID

入力関数2のDatID

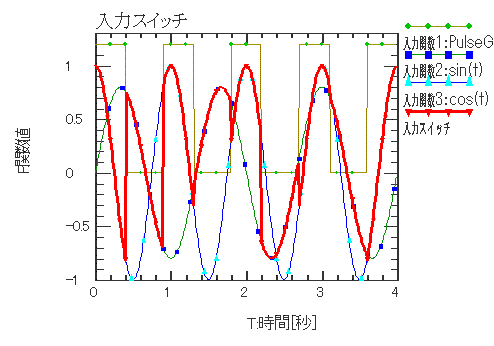入力関数　X1(t) = PulseGenerator(t) = 1.2*Pulse(0, 0.5, 1)
入力関数　X2(t) = sint(t) = Sin(0, 0.8, 270, 0)
入力関数　X3(t) = cos(t) = Cos(0, 1, 360, 0)
入力スイッチ　F(t) = Quantizer(X1(t), X2(t). X3(t))

スイッチング系関数

関数スイッチ

3つの入力関数をスイッチ用入力関数の正・ゼロ・負によってスイッチングします。

関数名

式

パラメータ 4個

No.

記号

既定値

説明

FunctionSwitch
FuncSw

F(x1,x2,x3,x4) = x2(t)	: x1(t) ＜ 0
F(x1,x2,x3,x4) = x3(t)	: x1(t) = 0
F(x1,x2,x3,x4) = x4(t)	: 0 ＜ x1(t)

スイッチ用入力関数のDatID

入力関数1のDatID

入力関数2のDatID

入力関数3のDatID

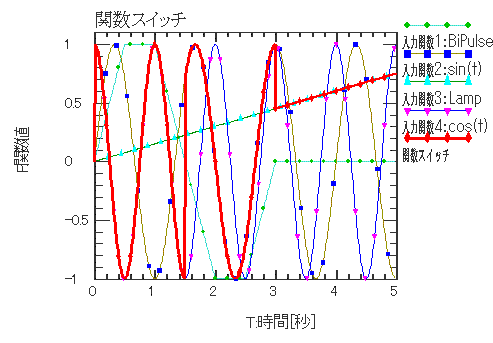入力関数　X1(t) = BiPulse(t)
入力関数　X2(t) = sint(t)
入力関数　X3(t) = Ramp(t)
入力関数　X4(t) = cos(t)
関数スイッチ　F(t) = FunctionSwitch(X1(t), X2(t). X3(t), x4(t))

スイッチング系関数

ディレイ

入力関数を遅延します。値保持のため、遅延タイムステップ分のメモリを要します。
▼この関数はリスタートを跨いで使用した場合、リスタート前の遅延時間の情報は失われますので、
リスタート計算には利用しないで下さい。

関数名

式

パラメータ 3個

No.

記号

既定値

説明

Delay

F(x1) = y2	: 0 ≦ t ＜ t3
F(x1) = x1(t – t3)	: t3 ≦ t

スイッチ用入力関数のDatID

0.0

遅延中の値

0.0

遅延時間

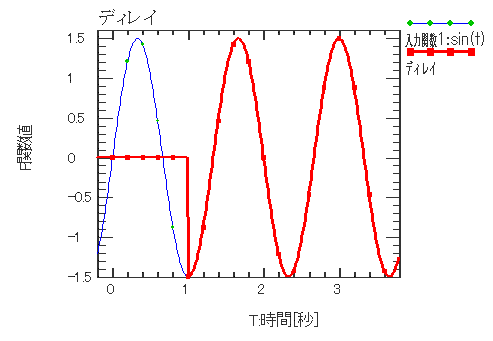入力関数　X1(t) = sin(t)
ディレイ F(t) = Delay(X1(t), 0, 1)

スイッチング系関数

ゼロ値保持

スイッチが入っている間(x1(t)＞0)は入力関数2(F(t)=x2(t))と同じ変化をしますが、切れた瞬間(x1(t’)≦0になったとき)の
x2(t’)値を保持します。値保持のため、メモリを要します。
値保持のため、倍精度実数のメモリを要します。
▼この関数はリスタートを跨いで使用した場合、リスタート前の遅延時間の情報は失われますので、
リスタート計算には利用しないで下さい。

関数名

式

パラメータ 2個

No.

記号

既定値

説明

ZeroOrderHold
FOH

F(x1,x2) = x2(t’)	: x1(t’+Δ)＞0→x1(t’)≦0のときのx2(t’)の値
F(x1,x2) = x2(t)	: x1(t) = 1のとき、x2(t)が出力
F(x1,x2) = 0	: x1(t) = 0のときの初期値

スイッチ用入力関数のDatID

入力関数2のDatID

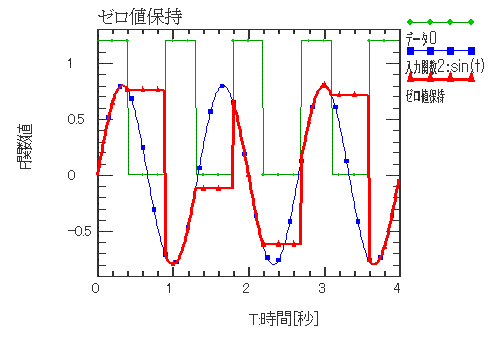入力関数　X1(t) = PulseGenerator(t)
入力関数　X2(t) = sint(t)
ゼロ値保持 F(t) = ZeroOrderHold(X1(t), X2(t))

スイッチング系関数

コンパレータ

2つの関数値を比較してオン(=1)・オフ(=0)します。
x1≧x2のときスイッチオン
x1＜x2のときスイッチオフ

関数名

式

パラメータ 2個

No.

記号

既定値

説明

Comparator
Comp

F(x1,x2) = 0	: x1(t) ＜ x2(t)
F(x1,x2) = 1	: x1(t) ≧ x2(t)

入力関数1のDatID

入力関数2のDatID

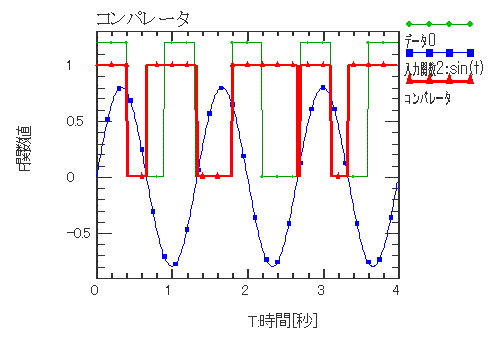入力関数　X1(t) = PulseGenerator(t)
入力関数　X2(t) = sint(t)
コンパレータ F(t) = Comparator(X1(t), X2(t))

出力系関数

「時系列関数」の出力系関数は、運動方程式による練成計算のフィードバック関数として用いられます。以下にその関数の仕様を示します。

2022年9月、現在、実装されているのは、応力関数とトルク関数だけです。

出力系関数表

表1. 応力関数

出力系関数

応力関数頁の先頭に戻る

QSfセルで計算した応力を時系列関数化して運動方程式の力として利用できるようにします。

関数名

式

パラメータ3個

No.

記号

既定値

説明

OFncForce
OFFC

Fr = ΣFri

nKind

固定

nID

QSfのセル番号

nComp

nComp=1/2/3=X成分/Y成分/Z成分

表2. トルク関数

出力系関数

トルク関数頁の先頭に戻る

QSfセルで計算したトルクを時系列関数化して運動方程式のトルクとして利用できるようにします。

関数名

式

パラメータ3個

No.

記号

既定値

説明

OFncTorque
OFTQ

Tq = ΣTqi

nKind

固定

nID

QSfのセル番号

nComp

nComp=1/2/3=X成分/Y成分/Z成分

株式会社シフトロックの最新情報をお届けします

@vektor_inc

カテゴリー: 技術情報

時系列関数の記述法

はじめに

時系列関数の生成

ジェネレータ系関数

数学系基本関数

スイッチング系関数

出力系関数

ホームページをリニューアルしました。

MRIの磁気シールドルーム