■はじめに
ここでは「Qm」の動磁場の機能で特長のあるものついて、ほんの一部ですがご紹介いたします。
応用例として「方形波電源のLR, CR回路の過渡応答の例」もご参照下さい。
■1.0 時系列関数の生成
動磁場解析では時系列データが出力されます。 時系列データの候補としては、電流・電圧・磁場・座標・速度。加速度等の時々刻々変化があります。 これらは、出力だけではなく、外部入力条件としても与えたい場合もあります。
つまり、動磁場解析では入力データに関しても時系列データをうまく取り扱わねばなりません。
単純な変化の場合は、タイムステップごとに入力できるでしょうが、少し複雑な変化になると、データ作成 手間が大変です。 また、エクセル等でソルバー外部でデータを作成していると、ソルバー側のタイムステップ幅の変えた場合、 再サンプリングの必要があるのですが、うっかり間違ってしまうことがあります。 間違いなく、複雑な条件を入れるためには、ソルバー自体に汎用的な関数発生や合成のメカニズムが必要です。
Qm動磁場版では、これらを解決するため、制御・数学等でよく用いられる関数を30数個用意し、それらを四則演算・合成できる 機能を持っています。
用意された関数を以下に紹介いたします。
関数群は機能別に、
- ジェネレータ系関数 ... 制御工学で使う基本的な関数
- 数学系基本関数 ... 数学で使う関数。 関数電卓にあるものが中心。
- スイッチング系関数 ... 他の関数と接続することにより、条件回路が組める関数。
- 出力系関数 ... 計算結果をフィードバックさせるために使用する関数。
があります。
もちろん、これらの関数の事前プロット・サンプリングの様子を含めたグラフ作成機能もあります。
■1.1 ジェネレータ系関数
ジェネレータ系関数は電流・電圧・速度・加速度などのソース(発生源)となるものが用意されています。
以下にその関数の仕様を示します。
ジェネレータ系関数選択画面
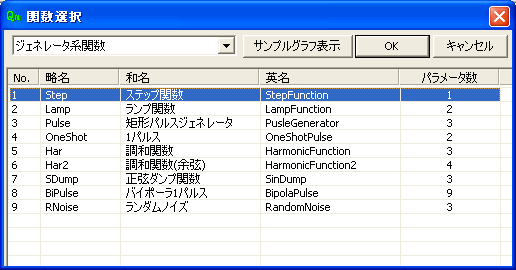
Qmでは、上記画面の「グラフ表示」のボタンを押せば、これから使う関数のサンプルプロット図が得られます。 下記関数表説明の図をクリックするとその拡大図が表示されます。
実際のシミュレーションでは、Qmの別の画面でサンプリングプロット図見ながら、これらの関数を式で合成します。
ジェネレータ系関数表
|
関数名
|
パラメータ 入力順に0,1.. 番号添付 |
|
記号
|
既定値
|
説明
|
|
StepFunction
Step
|
t1:遅延時間
|
0
|
ステップ関数

|
|
LampFunction
Lamp
|
t1:遅延時間
a2:傾き
|
0
1
|
ランプ関数

|
|
PulseGenerator
Pulse
|
t1:遅延時間
w2:パルス幅
p3:周期
|
0
1
2
|
矩形パルスジェネレータ

|
|
OneShotPulse
OneShot
|
t1:遅延時間
w2:パルス幅
|
0
1
|
1パルス

|
|
HarmonicFunction
Har
|
t1:遅延時間
w2:角速度
p3:位相
|
0
360
0
|
調和関数
周期 360/w1

|
|
HarmonicFunction2
Har2
|
B1:バイアス値
A2:振幅
n3:振動数
p4:位相角
|
0
1
60
0
|
調和関数(余弦)

|
|
SinDump
SDump
|
t1:減衰率
c2:中心
w3:半周期
|
1
1
1
|
正弦ダンプ関数
|
|
BipolaPulse
BiPulse
|
t1:
節点
t2:
節点
t3:
節点
t4:
節点
t5:
節点
t6:
節点
t7:
節点
a8:パルス頂
a9:パルス底
|
0
0.1
0.3
0.6
0.8
1.1
1.4
1
-0.8
|
バイポーラ1パルス(台形波) 
|
|
RandomNoise
RNoise
|
t1:遅延時間
w2:発生時間
s3:乱数シード
|
0
1
0
|
ランダムノイズ
注意:サンプリングごとに 0<ξ<1の一様乱数が発生します。 従いまして、変化は1/Δtで生じます。 乱数シード
s3=0のときは時間がシードとして採用されます。 複数の RamdomNoise関数を使用しますと最初に呼ばれた関数のみシードを使用します。
|
■1.2 数学系基本関数
数学系基本関数は関数電卓で使用する基本的な関数が用意されています。 これらの関数の四則演算記述することができますが、なるべく簡単な入力で複雑な式を入力できるように、多くの関数はそれ自身のパラメータとして、オフセットと大きさを持っています。
数学系基本系関数選択画面
数学系基本関数表
|
関数名
|
式
|
パラメータ 入力順に0,1.. 番号添付
|
|
記号
|
既定値
|
説明
|
Stack
(
|
(...
|
なし
|
|
新たな式を始めます。 それまでの式はスタックされます。(push) 開き括弧のような効果があります。
|
|
Evaluate
)
|
...)
|
なし
|
|
四則演算結果を評価し関数化します。直前に四則演算の結果が必要です。 閉じ括弧のような効果があります。 スタックがあれば引き出します。(pop)
|
Power
|
y = y1 + A2*tn3
|
y1:オフセット
A2:大きさ
n3:べき乗
|
0
1
2
|
べき乗
|
Sin
|
y = y1 + A2*sin(w3*t+p4)
|
y1:オフセット
A2:振幅
w3:角速度
p4:位相角
|
0
1
360
0
|
正弦
|
Cos
|
y = y1 +
A2*cos(w3*t+p4)
|
y1:オフセット
A2:振幅
w3:角速度
p4:位相角
|
0
1
360
0
|
余弦
|
Tan
|
y = y1 +
A2*tan(w3*t+p4)
|
y1:オフセット
A2:振幅
w3:角速度
p4:位相角
|
0
1
360
0
|
正接
|
Arsin
|
y = y1 +
A2*arcsin(t) :
-1≦t≦1
|
y1:オフセット
A2:大きさ
|
0
1
|
逆正弦
-1≦t≦1 の範囲外は鏡像対称の周期境界。
|
Arcos
|
y = y1 + A2*arccos(t) :
-1≦t≦1
|
y1:オフセット
A2: 大きさ
|
0
1
|
逆余弦
-1≦t≦1 の範囲外は鏡像対称の周期境界。 |
Atan
|
y = y1 +
A2*arctan(t)
|
y1:オフセット
A2: 大きさ |
0
1
|
逆正接
|
|
Exponential
Exp
|
y = y1 +
A2*exp(t)
|
y1:オフセット
A2: 大きさ
|
0
1
|
e指数
|
Log
|
y = y1 + A2*Log a3( t - t4 )
|
y1:オフセット
A2 :大きさ
a3 :底
t4:開始限界点
|
0
1
10
0
|
対数
|
Log10
|
y = y1 + A2*Log10 ( t - t3 )
|
y1:オフセット
A2 :大きさ
t3:開始限界点
|
0
1
0
|
常用対数
|
Ln
|
y = y1 + A2*Ln( t
- t3 )
|
y1:オフセット
A2:大きさ
t3:開始限界点
|
0
1
0
|
自然対数
|
|
Inv
|
y = 1 /(A2*(t-t3)+ y1)
|
y1:逆オフセット
A2:大きさ
t3:
|
0
1
0
|
逆数
|
|
GaussianFunction
Gaus
|
y = y1 +
A2*exp(-(t-c3)^2/(2*w4^2))
|
y1:オフセット
A2:振幅
c3:ピーク位置
w4:半値幅
|
0
1
0
1
|
ガウス関数
|
■1.3 スイッチング系関数
スイッチング系関数は入力となる関数x0,x1,..,を他の関数データで指定し、スイッチング(フィルタリング)します。 数学的には必ず合成関数になります。 他の物性値(物性番号で指定)からも入力を与えることができます。 スイッチング系以外のこれまでの関数でも、合成関数(たとえば
y=Exp(Sin(t))) を作ることができますが、そのままでは、他の物性値を関数入力にすることはできません。 ただし、スイッチング関数のInpを介せば、y=Exp(Inp(他の物性番号)) とすることができます。
スイッチング系関数選択画面
■1.4 複雑な時系列関数の合成
これまでの関数を使い、四則演算・合成関数などで、入力に使用したい時系列関数を合成します。 下記の画面はその例です。 各関数のパラメータの設定・関数間の演算子はセルを編集します。 使用できる演算子等はドロップダウンリストの中から選択します。 合成した関数の数式はリアルタイムに下段「数式表現」ボックスで表示されます。
この例では、InputSwitch関数により条件回路を組んでいます。
複雑な関数の時系列関数の合成編集画面
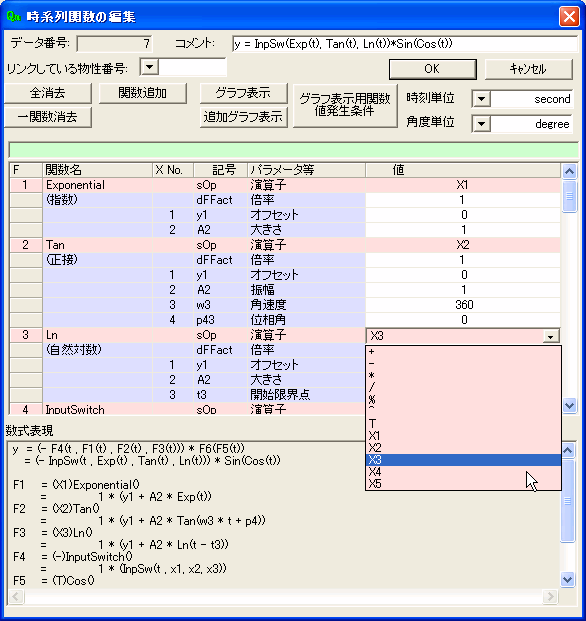
InputSwitch関数の仕様は以下のとおりです。
| スイッチング系関数 |
| 入力スイッチ |
入力関数x1(t) の値によって出力をx2(t), x3(t)にスイッチングします。
|
| 関数名 |
式 |
パラメータ 3個 |
| No. |
記号 |
既定値 |
説明 |
InputSwitch
InpSw |
| F(x1,x2,x3) = x2(t) |
: x1(t) ≦ 0 |
| F(x1,x2,x3) = x3(t) |
: 0 < x1(t) |
|
1 |
x1 |
0 |
スイッチ用入力関数のDatID |
| 2 |
x2 |
0 |
入力関数1のDatID |
| 3 |
x3 |
0 |
入力関数2のDatID |
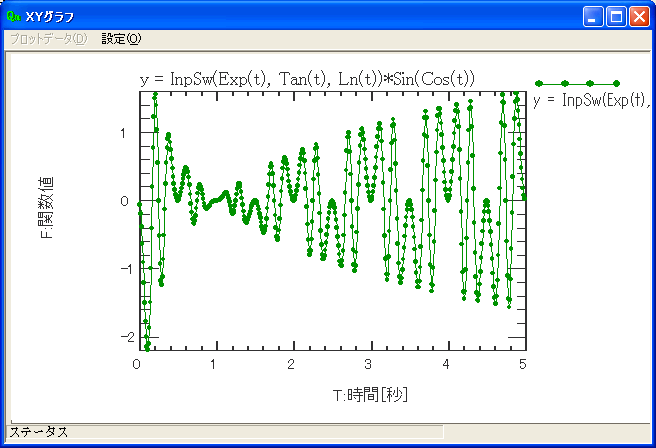
■1.5 シミュレーションで用いるサンプリンググラフの確認
この例の場合、実際の計算に用いるグラフは次のようになります。
下図の緑色の丸が設定されているタイムステップ幅でのサンプリング点となります。
合成した関数のサンプリンググラフ確認
|